A Contemporary Version of the Autostigmatic Microscope and Its Uses
OUTLINE
- What is an autostigmatic microscope (ASM)
- Measuring the radius of curvature of a concave surface
– Main historical use - Modern version of an ASM uses internal infinite conjugate optics
- Use of an ASM for alignment of optical systems
- Other uses of an ASM
- Conclusions
DESCRIPTION OF AN ASM

First description in English literature is Drysdale, Trans. Opt. Soc. London, 1900

Fig. 2 from the Drysdale paper of 1900

Further from the Drysdale paper
CAT’S EYE AND CONFOCAL FOCI

CAT’S EYE
Cat’s eye reflection
- Objective focused on surface
- Out going rays re-enter on opposite side of objective
- If surface tilted, reflected rays parallel outgoing rays in collimated space
- Cat’s eye used for setting crosshairs
- Cat’s eye used for setting reference

CONFOCAL FOCI
Confocal reflection
- Rays focused at center of curvature
- Rays hit surface at near normal incidence and re-trace themselves
- If surface tilted, rays do not re-trace and will not center on crosshairs
- Confocal used for alignment
- Confocal for bringing CofC to reference
EXAMPLES OF CAT’S EYE AND COFC SPOT IMAGES

OUT OF FOCUS CAT’S EYE SPOT IMAGE

IN FOCUS CAT’S EYE
Notice Shutter and Gain with focus
Locating an ephemeral point in space with 3 degrees of freedom to μm precision

OUT OF FOCUS & DECENTERED COFC SPOT

IN FOCUS BUT DECENTERED COFC SPOT

IN FOCUS AND CENTERED COFC SPOT
MEASUREMENT OF RADIUS OF CURVATURE
CONSISTS OF THREE STEPS:
- Focus on the concave mirror surface to get a Cat’s eye reflection
Set the reticle or electronic cross hairs on the reflected point image
This established the optical axis of the ASM - Move the ASM back to near the center of curvature of the concave mirror
Locate the reflected focused spot which may not be aligned to the objective
Tilt the mirror until the reflected focused spot enters the objective
Focus the ASM on the reflected spot and center it on the crosshairs
Note the distance of the ASM on a linear scale - Move the ASM forward until it is focused on the mirror surface
Moving from center of curvature means moving on a normal to the surface
Get a sharp focus the Cat’s eye reflection
Cat’s eye reflection will necessarily be centered on the cross hairs
Read the distance of the ASM on the linear scale
The difference of the Cat’s eye and confocal positions is the radius of curvature of the mirror
MEASUREMENT OF RADIUS OF CURVATURE

- Focus on surface, used Cat’s eye reflection to set crosshairs
- Move to confocal, adjust microscope so reflected spot in focus and centered on crosshairs, note linear scale reading
- Move to focus on surface and get well focused Cat’s eye spot. Note scale reading
Difference in readings is the radius of curvature
If this concept is well understood all other applications are easy
MEASUREMENT OF LONG RADIUS OF CURVATURE
USE DEFOCUSED COLLIMATOR
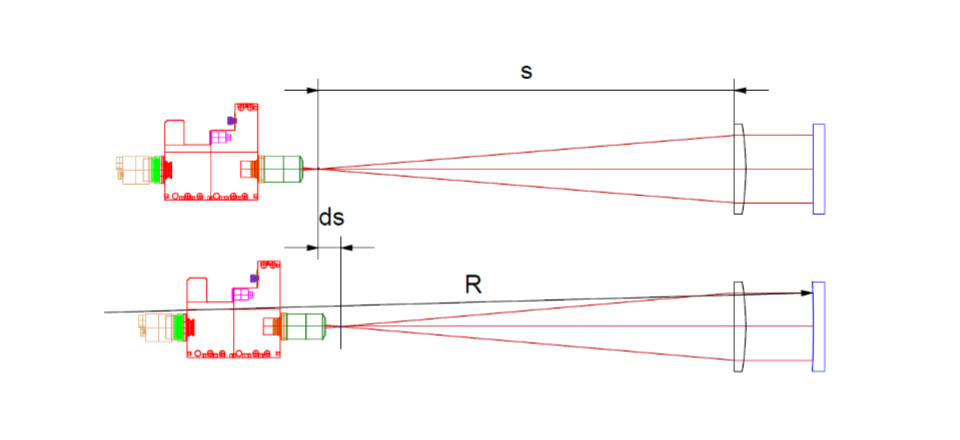
- Find s by putting a plane mirror in front of collimator
- Put long radius surface in front of collimator and note ds
- Since to first order efl = s, 1/s = 1/(s – ds) + 1/R, we find R = -s(1 + (s/ds))
(Be careful of signs, use common sense)
A CONTEMPORARY VERSION OF THE ASM
IS THREE INSTRUMENTS IN ONE

- Autostigmatic microscope
- Internal SM fiber source
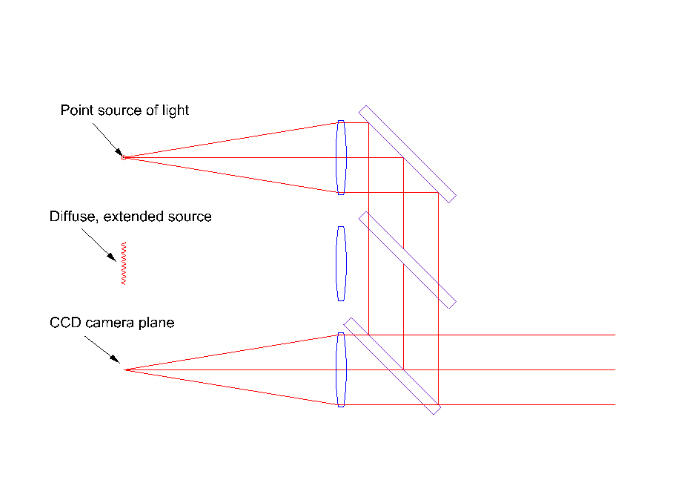
- Electronic autocollimator
- Simply remove objective

- Video imaging microscope
- Image plane parafocal with ASM focus
- Internal LED Kohler source
SOME ADVANTAGES OF THE CONTEMPORARY DESIGN
Use of solid state light sources – compact, internal, low heat, monochromatic
SM fiber coupled laser diode – bright for ease of alignment, near perfect spot
Video camera – ergonomic, high position sensitivity, settable reference
Software – permits high resolution centroiding on reflected spot
- Large dynamic range on reflected light intensities
- Recording and storage of Star images for optical quality determination
- Centroid data easily coupled into other scales, a CMM, for example
OTHER USES OF THE ASM; DESIGNED FOR ALIGNMENT
Perfect for locating centers of curvature and foci of optical systems
Use as a sensor on a centering station using a rotary table to define an axisUse was to align the elements of a f-theta laser scanner lens to a common axis
Lens system had spherical and toroidal lenses and an “off-axis” mirror
ASM mounted to the ram of a coordinate measuring machine
Used a large x, y, z stage to pick up centers of curvature and align to axis

- Don’t think like a lens designer and where rays go
- Think about where centers of curvature should go and how to get them on a common axis
USE TWO ASM’S TO ALIGN AN “OFF-AXIS” LENS


Radius of convex side longer than working distance of objective, need extra lens
SET-UP USING 2 ASM’S TO ALIGN LENS

ALIGNMENT OF FOLD MIRRORS

Plane fold mirrors have 3 degrees of freedom, 2 tilt and one displacement<
Optical and mechanical design will show where the center of curvature should be located when the fold mirror is proper aligned
A ball in a fixture will mechanically locate this position, and ASM can verify
ANOTHER EXAMPLE OF A FIXTURE FOR ALIGNMENT

THE ROLE OF STEEL BALLS IN ALIGNMENT
Steel balls are a physical realization of a point in space
Something you can physically touch as opposed to a theoretical object
The ball center, the “point”, defines 3 translational degrees of freedom in space
The ASM transfers an optical point, a CofC or focus, something you cannot touch, to the center of a ball, something that can be located physically
Steel balls are inexpensive, extremely precise and come in many sizes
Grade 5 chrome steel balls are round to 125 nm and cost about $3 each
Can be thought of as convex optical grade mirrors
Plug gauges are the cylindrical equivalent of balls and define axes in 3 DofF
(Plug gauges are Go/no go pins for gauging the size of holes)
ALIGNMENT USING ABERRATIONS
An ASM is a “Star” test device showing the point spread of an aberrated wavefront
It has sensitivity to about lambda/8 or lambda/10
Useful for quick check of quality of optical surfaces as they are assembled into systems
Alignment of a parabola as an example

Initially the return spot will not be centered on the crosshairs of the ASM
The parabola or autocollimating mirror are tilted until return spot on crosshairs
ALIGNMENT USING ABERRATIONS (CON’T)
When return spot lies on the crosshairs, the rays strike the flat at normal incidence
However, the normal to the flat may not be parallel to axis of parabola
As a consequence, the return spot will show coma

To finish the alignment, tilt the flat while keeping return spot on the crosshairs until the coma is reduced to a symmetrical spot.
The entire alignment process takes only minutes to accomplish
OTHER USES OF AN ASM – FINDING LENS CONJUGATES

FINDING FIRST ORDER LENS CONJUGATES
Finding the radius of curvature of one side is direct measurement
This assumes it is concave or there is sufficient working distance
Almost any lens can be reversed and measured through the side if not enough working distanceTo find the other conjugates it is necessary to model with a lens design program
Or use first order equations and an iterative equation solving program
See Parks, R. E., “Measuring the four paraxial…, Appl. Opts., 54, 9284 (2015)
ZERO INDEX MATERIAL – A USEFUL TRICK
When using an ASM or an interferometer most setups are double pass
Light comes from the instrument, reflects at normal incidence off the last surface and retraces itself back into the instrument
For a quick insight to the test it is a lot of work to trace a double pass system
The trick; reverse the system and make rays leave the last surface at normal incidence
To do this have rays from infinity travel through a medium of 0 index to the last surface
Then n*sin(θ) = n’*sin(θ’) = 0, so θ’ = 0, or the rays leave the last surface normal to it!
Now a marginal ray height solve after the last refraction shows the paraxial focus

Credit for the idea; I don’t know who deserves it
I learned it from Jim Burge at UofA, Optical Sciences
I suspect he may have learned it from Roland Shack
If someone knows a better attribution I like to know.
AN EXAMPLE – FINDING COFC’S AND SURFACES
Assume a simple optical system such as an air spaced doublet
Find the centers of curvature and surfaces vertices looking into the system
Reverse elements, object at infinity and n = 0, float by stop on last surface
MRH = 26.403 = 24.395 = 39.445 = -94.453
Object on first surface, image space f/# large, stop on last surface
MRH = -7.471 = -5.492 = -3.368 = 0
FIND THE INDEX OF REFRACTION OF A BALL
For small angles a = h/2r, and the normal = 2a, so the refracted ray angle is an/2
The ray angle relative to the x axis is 2a – an/2 = a(1-n/2)
The mrh = h/(h/r(1-n/2)) = 2r/(2-n)

Or, n = 2(mrh – r)/mrh
Works even if ball behind a window in a thermal chamber, but use ray trace
FIND THE INDEX OF A LIQUID AND RADIUS OF A SUBMERGED SURFACE

MEASUREMENT OF ANGLE

As shown earlier, by simply removing the objective the ASM is an autocollimator with sub-arc second sensitivity
The bright mode of the laser source makes initial alignment easy in ambient light
The small beam size makes it particularly useful for inspecting small prisms
ASM’S AND COMPUTER GENERATED HOLOGRAMS
A CGH pattern can simulate a ball, that is focus light a specific distance above the CGH
If balls are used to kinematically locate a CGH, a pattern to locate the balls can be included as part of the overall pattern. Then an ASM can precisely locate the balls. The balls, cemented in place, become an integral part of the CGH test artifact.
Because a CGH pattern can simulate a ball, a CGH can be made as an artifact for locating a group of points in space precisely located to < 1 μm in 3 dimensions.
An ASM mounted on a robot arm, for example, could be used to pick up the points one at a time to train and calibrate the robot.
EXAMPLE OF CGH HOLOGRAM

Printed on a 150 mm square photomask substrate
Each circular pattern produces points several distances above the CGH
Actual photograph is not available at the moment
CGH courtesy of Arizona Optical Metrology, LLC, www.cghnulls.com
CONCLUSIONS
While autostigmatic microscopes (ASM) are over 100 years old, modern technology makes them truly practical for many diverse optical metrology needs.
Once the basic operation of measuring the radius of curvature with an ASM is understood, it becomes obvious that an ASM has many more useful applications.
Almost everything discussed here can also be done with an interferometer with greater precision. However, if the ultimate in precision is not needed the ASM is more convenient to use because of its small size, light weight and ease of mounting. Further, in some applications the greater coherence of an interferometer make some of the applications more difficult to perform because of multiple fringe patterns.
In many instances an ASM is a cost effective and easy to use alternative to an interferometer.
USA

Innovations Foresight
4432 Mallard Point,
Columbus, IN 47201 USA
Telephone:
1-215-884-1101
Contact:
Customerservice@
All Asian Countries Except China

清 原 耕 輔 Kosuke Kiyohara
清原光学 営業部 Kiyohara Optics / Sales
+81-3-5918-8501
opg-sales@koptic.co.jp
Kiyohara Optics Inc.
3-28-10 Funado Itabashi-Ku Tokyo, Japan 174-0041
China

Langxin (Suzhou) Precision Optics Co., Ltd
1st floor, Building 10, Yisu Science and Technology Innovation Park, 100 meters west of the intersection of Xinhua Road and Weimeng Road, Kunshan City, Suzhou City, Jiangsu Province, 215345
Telephone: +860512-57284008
Contact: Wang Zengkun
+8617090133615
wangzengkun@langxinoptics.com
Copyright ©
Website by CS Design Studios
Headquarters: 7011 E Calle Tolosa, Tucson, AZ 85750
Laboratory: 1661 S Research Loop, Tucson, AZ 85710
